

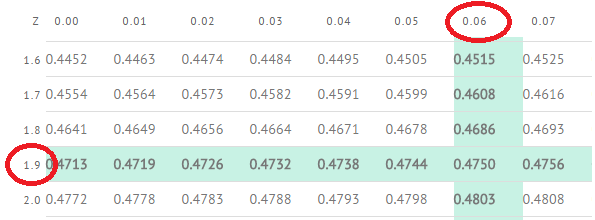
This is presented in (Figure) for the example in the introduction concerning the number of downloads from iTunes. The level of confidence of a particular interval estimate is called by (1-α).Ī good way to see the development of a confidence interval is to graphically depict the solution to a problem requesting a confidence interval. Levels less than 90% are considered of little value. Common convention in Economics and most social sciences sets confidence intervals at either 90, 95, or 99 percent levels. In reality, we can set whatever level of confidence we desire simply by changing the Z α value in the formula. Then read on the top and left margins the number of standard deviations it takes to get this level of probability. Divide either 0.95 or 0.90 in half and find that probability inside the body of the table. These numbers can be verified by consulting the Standard Normal table.

If we set Z α at 1.64 we are asking for the 90% confidence interval because we have set the probability at 0.90. If we chose Z α = 1.96 we are asking for the 95% confidence interval because we are setting the probability that the true mean lies within the range at 0.95. Z α is the number of standard deviations lies from the mean with a certain probability. The confidence level is defined as (1-α). α is the probability that the interval will not contain the true population mean. The analyst must decide the level of confidence they wish to impose on the confidence interval. This is where a choice must be made by the statistician. Notice that Z α has been substituted for Z 1 in this equation.
This is the formula for a confidence interval for the mean of a population.


 0 kommentar(er)
0 kommentar(er)
